Euler's Formula for Quantum Computing Beginners

I’m taking a break from working on my linear algebra cheat sheets to focus on a particular topic that I originally had a bit of trouble with.

The quantum computing textbook I’m working through mentions Euler’s formula a few times, but I was missing some background knowledge I needed in order to feel like I really understood the concept and how it was relevant. I ended up needing to search elsewhere for some supplementary resources, but now that I have a more solid grasp, I thought I would save y’all the trouble and synthesize the information into a blog post.

I’ll be using concepts like the imaginary number, complex numbers, the complex plane, etc. so if you need a refresher on these before getting started with this post, I suggest checking out the second post in my Linear Algebra For Quantum Computing Series before moving forward.

Otherwise, let’s go!

---

SHort intro to euler’s formula

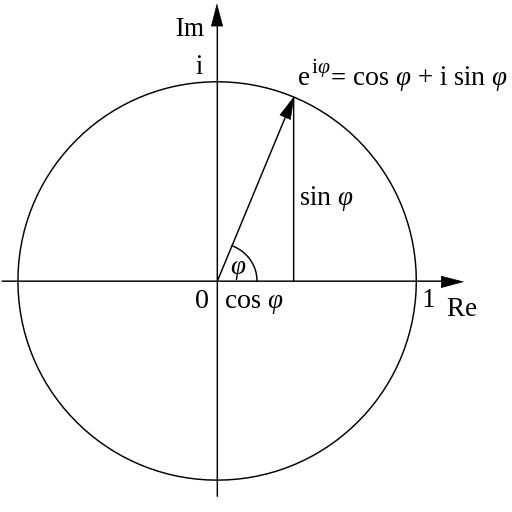
A complex number z that has a radius of 1 (meaning it lives on the unit circle) and an angle theta can be expressed with Euler’s formula in the following way:

$$ z = e^{i\theta} = \cos(\theta) + i\sin(\theta) $$

Visually, this can be represented like so (theta is replaced with phi here):

In the above figure, where the black line with the arrow ends is where z sits on the unit circle, and the length of said black line is 1 (this is the radius, we’ll call it r from now on).

---

Laying the groundwork for euler’s formula

Before we get in to what’s going on with the mathematical constant e in Euler’s formula, also called Euler’s number or the natural number, let’s focus just on this part:

$$ z = \cos(\theta) + i\sin(\theta)$$

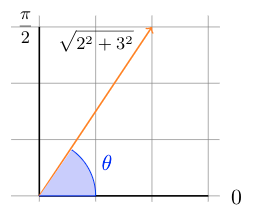
If z takes the form of a + bi, and z = 2 + 3i, then on the complex plane that would look like:

So to find the length of the radius, we can use the Pythagorean theorem:

$$ r^2 = a^2 + b^2 $$ $$ r = \sqrt{a^2 + b^2} = \sqrt{13}$$

And to find the angle theta, we can do the following:

$$\tan(\theta) = \frac{b}{a} = \frac{3}{2} $$ $$ \arctan(\tan(\theta)) = \arctan(\frac{3}{2}) $$ $$ \theta = \arctan(\frac{3}{2}) \approx 0.983 radians \approx 56.31^\circ $$

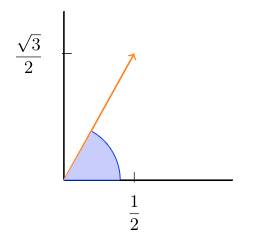
However, what if we are given the radius r and the angle theta, and need to work backwards to find a and b? Imagine that:

$$ r = 1 $$ $$ \theta = \frac{\pi}{3} $$

Using basic trigonometry, we can find that:

$$ \cos(\theta) = \frac{adjacent}{hypotenuse} = \frac{a}{r} $$ $$ r \cdot \cos(\theta) = a $$

And:

$$ \sin(\theta) = \frac{opposite}{hypotenuse} = \frac{b}{r} $$ $$ r \cdot \sin(\theta) = b $$

Since r = 1, we know:

$$ a = \cos(\theta) $$ $$ b = \sin(\theta) $$ $$ z = a + bi = \cos(\theta) + i\sin(\theta) $$

As you can see, we’ve made it to the spot we were trying to get to in this section, which is where:

$$ z = \cos(\theta) + i\sin(\theta) $$

In this case, the answer is:

$$ z = \frac{1}{2} + \frac{\sqrt{3}}{2}i$$

---

The natural number

The natural number, or e, is a constant and is roughly equal to 2.71828, which is visualized on the graph below:

This is the graph of the equation y = 1/x, and the area under the curve that is shaded-in blue is equal to 1, which is one thing that makes e special.

Another way it is special is that it is the sum of the following infinite series:

$$ 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} + ...$$

Which can be written as:

$$ \sum_{n=0}^{\infty} \frac{1}{n!} $$

The first number in the series tripped me up when I was studying originally, because I forgot that the following is true:

$$ \frac{1}{0!} = \frac{1}{1} = 1 $$

As a refresher to understand why this is the case, remember that

“…the definition of a factorial is the product of all integers equal to or less in value to the original number—in other words, a factorial is the number of combinations possible with numbers less than or equal to that number.

Because zero has no numbers less than it but is still in and of itself a number, there is but one possible combination of how that data set can be arranged: it cannot. This still counts as a way of arranging it, so by definition, a zero factorial is equal to one…”

---

PUTTING EVERYTHING TOGETHER WITH power series

So far, we have shown that there is an intrinsic relationship between complex numbers and trigonometry. We’ve also started to get an in idea of what e is.

Our next step is to recall the power series of the cosine and sine functions:

$$ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} - ... $$ $$ \sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} - ... $$

These are called Taylor series, and you’ll notice that cos(x) has only even powers while sin(x) has only odd powers. For now, it’s not super important to understand how these power series were derived, but if you’re curious for more information, I suggest checking out this resource from Khan Academy.

There is one more important Taylor series to know:

$$ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \frac{x^5}{5!} + ... $$

Which can also be expressed as:

$$ \sum_{n=0}^{\infty} \frac{x^n}{n!} $$

However, in Euler’s formula, the exponent on e is multiplied by the imaginary number i. What happens when we introduce i into the power series we just looked at?

$$ e^{ix} = 1 + ix + \frac{i^2x^2}{2!} + \frac{i^3x^3}{3!} + \frac{i^4x^4}{4!} + \frac{i^5x^5}{5!} + ... $$ $$ e^{ix} = 1 + ix - \frac{x^2}{2!} - \frac{ix^3}{3!} + \frac{x^4}{4!} + \frac{ix^5}{5!} - ...$$

Which can be rearranged to…

$$ e^{ix} = \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - ...\right) + \left(ix - \frac{ix^3}{3!} + \frac{ix^5}{5!} - ... \right) $$

And if we factor i out from the elements in the second set of parentheses, we get…

$$ e^{ix} = \left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} - ...\right) + i\left(x - \frac{x^3}{3!} + \frac{x^5}{5!} - ... \right) $$

Which, if you look closely, simplifies to exactly the trigonometric side of Euler’s formula!

$$ e^{ix} = \cos(x) + i\sin(x) $$

And this is Very Cool.

---

Why is this very cool?

There are many reasons why Euler’s formula is Very Cool, but one reason is that it “establishes the fundamental relationship between the trigonometric functions and the complex exponential function.” It is useful for differential equations, electrical engineering, signal processing, and other areas. Richard Feynman is said to have called it “the most remarkable formula in mathematics”. Aren’t you glad you read a whole post about it now?

By the way, Euler didn’t exactly get to this formula on his own - he built off some work by Roger Cotes and he would discuss the formula at various points with Johann Bernoulli.

In upcoming posts, we’ll look at matrices, what they are, how to work with them, and what happens when you introduce them to Euler’s formula (spoiler alert: everything works out).